Exposure Calculation Technique

In the single-beam transmission hologram setup, using a 5 mW helium neon laser with an output power of 5 mW at the aperture, a 10x microscope objective placed 43 inches from the plate holder, and a PFG-01 plate, the exposure time would be 20 seconds. This will give you an emulsion exposure density of 1.0, the optimal density for a bright transmission hologram. The acceptable density range for a bright transmission hologram is 0.8 to 1.2. I actually used the setup in Figure 16a to achieve these results.

If you can afford a handheld power meter ($450 from Edmund Optics), I recommend you get one. Using a power meter allows you to measure the intensity of a laser beam, diverged or undiverged, directly in watts/cm²-seconds. The meter has a push button which allows you to change the wavelength of the laser light you're measuring. In our case, 632.8 nm (nanometers). The actual setting on the meter would be 633 nm since the meter doesn't give fractions of a wavelength. There is also a push button for switching between milliwatts and microwatts (µW) as well as a slide-into-place filter for measuring power levels greater than 10 mW. Power readings are given in watts/ cm²-seconds.

Let's look at an example of using this meter in figuring out your exposure time for the single-beam transmission hologram. Set the meter to microwatts, wavelength set at 633 nm, and the filter not covering the sensor. Place the sensor area of the meter at the center of the plate holder facing the incoming diverging reference beam square on, that is, perpendicular to the beam. Take four separate readings and average them. Let's say the average is 4 µW/cm²-seconds.

Because the reference beam is incident on the plate at 56 degrees, you must take the cosine of 56 and multiple this number (0.5592) by 4: 0.5592 x 4 µW/cm²-seconds = 2.24 µW/cm²-seconds. This is the real power level (intensity) of the reference beam at the plate. Now you divide the power sensitivity of the PFG-01 recording plate by the calculated power reading at the plate holder: 80 µW/cm² ÷ 2.24 µW/cm²-seconds = 35.7 seconds. Your exposure time will be 36 seconds because you should always round up.

If you don't want to spend this much, you can use a volt-ohm-meter (VOM) connected to a small solar cell (both together about $60) to measure the light level at the plate holder in volts and use this measurement to indirectly calculate the exposure time. The sensitivity of holography plates and films are rated in microwatts per centimeter squared, not in ISO or ASA ratings. Unfortunately, you can't convert between these two sensitivity ratings. So you can't use a photographic light meter.

You will not be using this exposure calculation technique until the next section on Recording and Processing. It's presented here so you can become familiar with the technique and refer back to it when you need it during your recording. Here, I'll be telling you to make an exposure and to process the plate, but I'm actually referring to what you'll be doing in the next section on Recording and Processing. You will not be making the real exposure and processing at this time.

Figure 17a: Meter and solar cell connected.

• Using a VOM, connect its leads to the solar cell leads with positive to positive and negative to negative as shown in Figure 17a. Red is usually positive and black (or other color) is negative.
• Set the meter to its lowest direct current (DC) voltage range. If a negative sign shows up, reverse the leads. It really doesn't matter if you're getting a negative or positive reading. The amount of voltage should be the same.
• Place the solar cell at the center of the plate holder (white card removed) facing and perpendicular to the incident beam.
• Take note of the voltage reading, with the room lights off, and write it down. You will need a small flashlight to read the meter in the dark. Make sure the flashlight's light does not strike the solar cell.
• Expose the plate for 20 seconds.
• Process the plate only through the stop bath step, wash, and dry.

You're now going to measure the density of the dried hologram. With the room lights on, place the VOM on a table top with the solar cell attached and place the solar cell face up on the table top so the room lights illuminate the solar cell. Take a reading in volts of the ambient room light as shown in Figure 17a. We'll call this Intensity One (I₁). Write the voltage down on paper.

Next, place the dried, unbleached, exposed plate on top of the solar cell with the emulsion facing up (the emulsion side of the plate is less reflective than the glass side). Take a second voltage reading as shown in Figure 17b. We'll call this Intensity Two (I₂). Write this voltage down on paper. If you've used film instead of a plate, place the film down on the cell with the emulsion up and hold the film's four corners down with your two gloved hands to keep the film as flat as possible. If you were to use a clear glass plate to keep the film flat, the glass would reflect some of the light and give you an inaccurate reading.

Figure 17b: Meter and solar cell with plate on top.

Now divide the first voltage I₁ by the second voltage I₂. The resulting number is a ratio and does not have units. Using a Common Logarithms of Numbers table, look up this number and the corresponding log of that number is given and is your plate density. Or use a calculator to find the log of the ratio. The equation is:

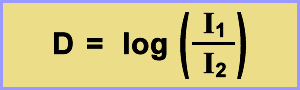
As an example, if I₁ is 24 volts and I₂ is 3 volts, then I₁ divided by I₂ is 8. The log of 8 is 0.9. This puts you within the density range of a properly exposed transmission hologram.

If you get a voltage reading of greater than 9.91 (which is the largest voltage number in the log table), you need to do some simple arithmetic to achieve the proper density reading. For example, if your dividend between I₁ and I₂ is 11 volts, find the log number for 9.91 volts and write it down (.9961). Next, subtract 9.91 from 11 giving you 1.09. Look up 1.09 as your voltage reading in the table and you will get .0453. Add .9961 and .0453 and you get 1.0414. You're within the density range of 0.8 and 1.2.

If your density is below this range, you need to increase your exposure time. If the density is above the range, you need to decrease your exposure. If your first exposure didn't fall within the range, keep making different exposure times until you've achieve a density within the range. Keep everything constant and only change the exposure time. Once you've achieved an exposure density within the acceptable range, you can use the original voltage measured at the plate holder as a reference for future setups and measurements with the VOM and solar cell at the plate holder.

For example, if your original measurement at the plate holder was 6 volts and your exposure time was 20 seconds and you achieved a plate density of 1.0, then a voltage reading of 6 volts at the plate holder of your next setup will give you a density of 1.0 for a 20 second exposure. If your voltage reading at the plate holder is 3 volts in a new setup, then your exposure time should double to 40 seconds. The relationship between the voltage reading and the exposure time is linear. I've included the Common Logarithms of Numbers table for your convenience.